En retrospectiva Resolución de balances de materia y de energía simultáneos

En esta sección describimos la forma de determinar el número de grados de libertad que intervienen en un proceso, e decir, el número de valores adicionales de variables que es preciso especificar para poder obtener la solución de un problema.

Qué clases de restricciones (ecuaciones) intervienen en el análisis de los grados de libertad? (V)

No contamos aquí con espacio para ilustrar otras combinaciones de unidades simples para formar unidades más complejas, pero Kwauk ha preparado varias tablas excelentes que resumen las variables y los grados de libertad para columnas de destilación, absorbedores, intercambiadores de calor y similares. Lea también las referencias citadas al final del capítulo.

Solución Grados de libertad en un sistema compuesto por varias unidades

Mezclador:

Ejemplo Grados de libertad en un sistema compuesto por varias unidades

Se produce amoniaco por reacción de N2 y H2:

N2 +  3H2 → 2NH3

La figura E6.5a muestra un diagrama de flujo simplificado. Toda las unidades excepto el separador y las tuberías son adiabáticas. El amoniaco líquido producido está prácticamente libre de N2, H2 y A. Suponga que el gas de purgado está libre de NH3. Considere que el proceso está formado por cuatro unidades individuales para un análisis de grados de libertad, y luego quite la variables redundantes y agregue las restricciones redundantes a fin de obtener lo grados de libertad del proceso global. La fracción de conversión en el reactor e del 25%.

Qué clases de restricciones (ecuaciones) intervienen en el análisis de los grados de libertad? (IV)

Podemos calcular los grados de libertad para combinaciones de procesos simples similares o distintos mediante una combinación apropiada de sus grados de libertad individuales. Al sumar los grados de libertad de las unidades, es necesario eliminar cualquier conteo doble ya sea de variables o de restricciones, y tomar en cuenta debidamente las corrientes interconectadas cuyas características a menudo se fijan únicamente por deducción.

Examine el mezclador-separador de la figura 6.3. Para el mezclador considerado como una unidad independiente, el ejemplo 6.1b, Nd = 2Nsp + 6. Para el separador, una unidad en equilibrio:

Figura Grados de libertad en unidades combinadas

Solución grados de libertad para el caso de múltiples reacciones

La figura E6.4 muestra el proceso; se supone que todas las corrientes son gases. Sólo dos de las reacciones son independientes. Q es una variable. Por sencillez suponemos que todas las corrientes que entran y que salen están a la misma temperatura y presión.

Ejemplos grados de libertad para el caso de múltiples reacciones

Se quema metano en un horno con 10% de aire en exceso; la combustión no es completa, así que sale algo de CO del horno, pero nada de CH4. Las reacciones son:

Solución grados de libertad cuando ocurre una reacción en el sistema

En los flujos F2 y W sólo podemos especificar cuatro composiciones; una quinta especificación es redundante. Los flujos totales se desconocen. El valor que se indica del agua en exceso proporciona la información acerca de los productos de la reacción. Sin duda es necesario especificar la tempertura y la presión, lo que da cuenta de dos grados de libertad. El grado de libertad restante podría ser la razón N2/H2 en P, o el valor de F2,, o la razón F1/F2, etcétera.

Ejemplo grados de libertad cuando ocurre una reacción en el sistema

Una reacción clásica para producir H2 es la llamada reacción de "desplazamiento de agua":

Qué clases de restricciones (ecuaciones) intervienen en el análisis de los grados de libertad? (III)

Hasta ahora hemos examinado unidades individuales en las que no ocurre reacción. Cómo se afecta Nd por la presencia de una reacción en la unidad? La forma como se calcula Nv no cambia. En cuanto a Nr, se restan de Nv todas las condiciones que representan restricciones indipendientes sobre la unidad. Así, el número de balances de materia no es por fuerza igual al número de especies (H2O, O2, CO2, etc.) sino que es el número de balances de materia independientes que hay, y se determina de la misma forma como los hicimos en la secciones 3.2 a 3.4. Por lo regular (aunque no siempre), este número e igual al número de balances elementales (H, O, C, etc). Las proporciones fijas de materiales comola de O2/N2 del aire o de CO/CO2 en un gas producto serán una restricción, como también lo será una fracción de conversión determinada o la velocidad de flujo molar de un material. si todavía quedan grados de libertad, la especificación incorrecta de una variable puede destruir la independencia de las ecuaciones y/o especificaciones previamente enumeradas para Nr, así que tenga cuidado.

Solución Ejemplo Especificación correcta de un proceso

Primero calculamos Nv y luego Nr. Suponemos que las temperaturas y presiones de todas las corrientes son idénticas. El número de variables Nv:

Ejemplo Especificación correcta de un proceso

La figura E6.2 muestra una columna de separación isotérmica. Actualmente, las especificaciones de la columna exigen que las fracciones e masa de la alimentación sean ωc4 = 0.15, ωc5 = 0.20, ω1c5 = 0.30 y ωc6 = 0.35; las fracciones de masa en lo domos son ωc5 = 0.40 y ωc6 = 0; y la fracción de masa del producto residual es ωc4 = 0. A menos que se especifique como 0, el componente está presente en una corriente.

Dado que F = 100lb/h, está completamente especificado el separador? Es decir, son los grados de libertad Nd = 0? Las corrientes P1 y P2 no están en equilibrio.

Ejemplo Determinación del número de grados de libertad de un proceso (VI)

e) Tanque (etapa) bien mezclado con dos fases en equilibrio

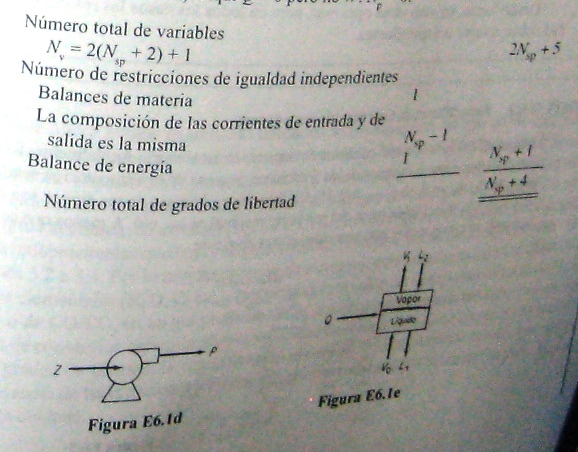
Fig. E6.1e (L, fase líquida; V, fase de vapor): Aquí W=0. Aunque hay dos fases (V1 y L1) en equilibrio dentro del sistema, las corrientes que entran y salen tienen una sola fase cada una. Con equilibrio queremos decir que ambas fases están a la misma temperatura y presión y que para cada componente se conoce una ecuación que relaciona la composición en una fase con la composición en la otra.

Ejemplo Determinación del número de grados de libertad de un proceso (V)

d) Bomba (Fig. E6.1D): Aquí Q= 0 pero no W: Np = 0

Ejemplo Determinación del número de grados de libertad de un proceso (IV)

c) Intercambiador de calor (Fig. E6.1c): Para este proceso suponemos que W = 0 (pero no Q)

Ejemplo Determinación del número de grados de libertad de un proceso (III)

Mezclador (Fig. E6.1b): Para este proceso suponemos que W = 0, pero no Q.

Ejemplo Determinación del número de grados de libertad de un proceso (II)

Divisor de Corriente (Fig. E6.1a): Suponemos Q = W = 0, y que en el proceso no interviene el balance de energía. Implícito en el divisor está el hecho de que las temperaturas, presiones y composiciones de las corrientes de entrada y de salida son idénticas. La cuenta del número total de variables, del número total de restricciones y de grados de libertad es la siguiente:

Ejemplo Determinación del número de grados de libertad de un proceso (I)

Consideramos cinco procesos típicos representados por sus respectivas figuras, y para cada uno plantearemos la pregunta: Cuántas variables es necesario especifica? [es decir, Cuántos grados de libertad (Nd) ha?] para que la resolución de los balances de materia y de energía combinados esté determinado? Todos los procesos serán en estado estacionario, y las corrientes que entran y salen consistirán en una sola fase.

Qué clases de restricciones (ecuaciones) intervienen en el análisis de los grados de libertad? (II)

Como ilustración del análisis de los grados de libertad, examine las figuras 6.2(A) y (B) que muestran un sencillo proceso isobárico e isotérmico en estado estacionario en el que participan tres corrientes y hay transferencia de calor. La cuenta de variables y restricciones es

La forma en que se especifican las composiciones no afecta el análisis.

Ahora consideramos cinco procesos sencillos en el ejemplo 6.1 y evaluaremos el número de grados de libertad para cada uno.

Qué clases de restricciones (ecuaciones) intervienen en el análisis de los grados de libertad? (I)

Por lo regular

1. balances de materia independiente para cada especie (se puede sustituir un balance total por el balance de una especie.)
2. balance de energía.
3. relaciones de equilibrio de fases, es decir, ecuaciones que indican las composiciones relativas de una especie que existe en dos (o más) fases.
4. relaciones de equilibrio químico. El número de estas ecuaciones es igual al número mínimo de relaciones estequiométricas independientes (véase el Apénd L) que pueden representar las especies presentes en una sola fase.
5. relaciones implícitas, como que la concentración de una especie es cero en una corriente.
6. relaciones explícitas, como que una fracción dada de una corriente se condensa.

Conceptos Análisis de los grados de libertad en un proceso de estado estacionario (IV)

Así pues, podemos concluir que el número de variables Nv requeridas para especificar por completo la condición de una corriente está dado por

Nv  = Nsp + 2    (6.2)

Debemos tener presente que en un sistema binario, por ejemplo, en el que un componente de la corriente es cero, por consistencia contamos Nsp = 2 y tratamos como restricción el hecho de que se componente tiene valor cero.

Conceptos Análisis de los grados de libertad en un proceso de estado estacionario (III)

Algunas variables se pueden sustituir por otras, como la temperatura por las entalpías específicas, y los flujos de las corrientes por la proporción del reciclaje.

Examine la corriente de flujo en la figura  6.1. Hay dos formas de especificar el número de variables asociadas a un flujo continuo (variables de flujo) (suponemos que la corriente es una sola fase en la que no ocurren reacciones; si hay más de una fase, cada fase se tratará como una corriente individual):

Conceptos Análisis de los grados de libertad en un proceso de estado estacionario (II)

En este capítulo, el análisis de los grados de libertad de un proceso parte de la suposición de que se trata de un proceso continuo en estado estacionario, como se acostumbra hacer un diseño. Si lo que interesa son las operaciones o el control, el análisis se basará  en un proceso en estado no estacionario y se tomará en consideración el término de acumulación. (Además, no todas las variables de un proceso pueden ajustarse, de modo que la selección de cuáles variables  se pueden especificar es limitada).

En el análisis se incluyen variables tanto extensivas como intensivas , en contraste con los grados de libertad que se obtienen de la aplicación de la regla de las frases. (Sec. 4.5) que contempla  sólo las variables intensivas. Qué clase de variables debemos considerar? Ejemplos típicos de ellas son:

1. Temperatura
2. Presión
3. Velocidad de flujo másico (molar) para cada componente de una corriente, o bien la concentración de cada componente más la velocidad de flujo total.
4. Entalpías específicas
5. Velocidad de flujo de calor, trabajo (en el balance de energía)
6. Proporción de reciclaje.

Conceptos Análisis de los grados de libertad en un proceso de estado estacionario (I)

Un aspecto importante de los problemas de balance de materia y de energía combinado es como asegurar que las ecuaciones de proceso o conjuntos de módulos estén determinados, es decir, tengan por lo menos una solución y, ojalá, no más de una solución. La pregunta es: Cuantas variables son incógnitas, y por ende de cuántas es necesario que se especifiquen los valores en cualquier problema? El número de grados de libertad es el número de variables en conjunto de ecuaciones independientes a los que es necesario asignar valores para poder resolver las ecuaciones.

Sean Nd el número de grados de libertad, Nv el número de variables y Nr el número de ecuaciones (restricciones). Entonces, para Nr ecuaciones independientes en general

Nd = Nv - Nr

y concluimos que es preciso especificar Nv - Nr variables siempre que las Nr ecuaciones sigan siendo independientes. No es necesario escribir todas las ecuaciones durante el análisis; sólo hay que identificarlas. No importa si las ecuaciones son lineales o no.

Temas por tratar Análisis de los grados de libertad en un proceso de estado estacionario

En esta sección explicaremos la forma de calcular los grados de libertad de un proceso continuo en estado estacionario.

Análisis de los grados de libertad en un proceso de estado estacionario

Sus objetivos al estudiar esta sección serán ser capaz de:

1. Identificar los nombres y números de las variables en los flujos que entran en una unidad de procesamiento y salen de ella, y las variables asociadas a la unidad misma.
2. Determinar el número de ecuaciones independientes para cada unidad de procesamiento y las restricciones.
3. CAlcular el número de grados de libertad (variables de decisión para unidades individuales y combinaciones de unidades con y sin la ocurrencia  de reacciones)
4. Especificar los valores de un número de variables igual al número de grados de libertad de una unidad.

Resolución de balances de materia y de energía simultáneos

Ahora que el lector ha adquirido cierta experiencia en la realización de balances de energía, ha llegado el momento de aplicar estos conocimientos a problemas más complejos en los que intervienen balances tanto de materia como de energía. Ya hemos presentado algunos ejemplos sencillos de balances de materia y de energía combinados, como el cálculo de la temperatura de reacción adiabática, en los que un balance de materia estableció las bases  para efectuar un balance de energía.

En  la sección 6.1 veremos cómo podemos asegurarnos de que un problema está correcto y completamente especificado mediante una extensión del análisis de grados de líbertad que ya tratamos en el cap 3. Posteriormente repasaremos la forma de utilizar códigos de computadora, y en particular los programas de simulación de procesos, para resolver problemas complejos.

Ideas Clave Diagramas de humedad y uso

1. Las cartas psicrométricas (de humedad) proporcionan información útil para efectuar balances de materia y energía en procesos de calentamiento, enfriamiento, humidificación, des humidificación, condensación y vaporización.
2. DAdos los valores de dos variables intensivas, los valores de todas las demás se pueden leer de las cartas (o de tablas, o calcularse por medio de códigos de computadora)

Retrospectiva Diagramas de humedad y uso

En esta sección describimos la estructura de las cartas de humedad y la información que se obtiene de ellas, y cómo pueden usarse en los balances de materia y de energía.

Solución Balances combinados de materia y de energía para una torre de enfriamiento

Los datos de entalpía, humedad y volumen húmedo para el aire, tomados de la carta de humedad, son los siguientes (vea la fig E5.26)