Ecuaciones no lineales independientes (I)

Los criterios precisos que se usan para comprobar si un sistema lineal de ecuaciones ésta determinado no se pueden extender sin más a los sistemas de ecuaciones no lineales. Además, la resolución de conjuntos de ecuaciones no lineales requiere el empleo de códigos de computadora que tal vez no puedan resolver el problema por diversas razones, algunas de las cuales mencionaremos aquí. El problema por resolver se puede escribir como:

donde cada función f1(x1,......, xn) corresponde a una función no lineal que contiene una o más de las variables cuyo valor se desconoce.

Ecuaciones no homogéneas - ejemplo 3

El número de componentes independientes no siempre es igual al número de especies atómicas, como se muestra en el siguiente ejemplo.

Determine el número de componentes independientes para un proceso en el que interviene la siguiente reacción:

Ecuaciones no homogéneas - ejemplo 2

Determine el número de componentes independientes (que es igual al número de balances de materia independientes) para un proceso en el que intervienen las dos reacciones en competencia siguientes:

Ecuaciones no homogéneas - ejemplo 1

Con objeto de ilustrar las operaciones elementales requeridas para aplicar el método de Gauss-Jordan, consideremos el siguiente conjunto de tres ecuaciones independientes con tres incógnitas:

Ecuaciones no homogéneas r > n (II)

En general, hay dos formas de resolver la ecuación (L.3) para x1,.......,x3: técnicas de eliminación y técnicas iterativas. Ambas se ejecutan fácilmente con la ayuda de programas para computadora. En la contraportada del libro el lector encontrará un disco con programas que pueden usarse para resolver conjuntos de ecuaciones lineales. Ilustraremos el método de eliminación de Gauss-Jordan. El lector puede encontrar otras técnicas en textos sobre matrices, álgebra lineal y análisis numérico.

La esencia del método de Gauss-Jordan consiste en transformar la ecuación (L.3) en la ecuacion (L.4) mediante operaciones elemantales secuenciales no únicas sobre la ecuación (L.3).

Ecuaciones no homogéneas r > n (I)

Ecuaciones no homogéneas r < n

Ecuaciones no homogéneas r = n

Ecuaciones homogéneas (todos los coeficientes del miembro derecho son cero) Ax = 0

Ecuaciones lineales independientes (IV)

Si ésta no es cuadrada, se buscará el determinante distinto de cero para la mayor de las matrices cuadradas que pueden formarse a partir de A. Es necesario verificar todas las posibles submatrices de A. Utilizaremos números enteros como elementos en las matrices que siguen. Los números no enteros pueden conducir a resultados menos claros en lo que toca a la verificación de si el valor de un determinante es cero o no.

Se r = número de ecuaciones independientes
n = número de variables cuyo valor se desconoce.

Ecuaciones lineales independientes (III)

La figura L.2 representa cada uno de estos casos de forma geométrica en dos dimensiones. El caso 1 por lo regular se considera inconsistente, en tanto que los casos 2 y 3 son consistentes. Sin embargo, para un ingeniero interesado en la resolución de problemas prácticos, el caso 3 es tan insatisfactorio como el caso 1. Por tanto, llamaremos el caso 2 determinado, y el caso 3 se calificará como indeterminado.

Para asegurar que un sistema de ecuaciones representando por (L.1) tenga una solución única, es necesario demostrar primero que que (L.1) es consistente, esto es, que la matriz de coeficiones A y la matriz aumentada [A, b] tienen el mismo rango, r. Entonces, si n = r, el sistema (L.1) será determinado. Por otro lado, si r < n, como puede suceder, será necesario especificar de alguna manera (n - r) variables, o fijarlas mediante procedimientos de optimización. Si las ecuaciones son independientes, m = r. Si calculamos el orden del determinante distinto de cero más grande de una matriz dada, podemos determinar el rango de es matriz.

Ecuaciones lineales independientes (II)

Con m ecuaciones de n variables incógnitas podemos distinguir tres casos:

1. No existe un conjunto de x que satisfaga la ecuación (L.1)
2. Existe un conjunto único de x que satisface la ecuación (L.1)
3. Existe un número infinito de conjuntos de x que se satisfacen la ecuación (L.1)

Ecuaciones lineales independientes (I)

Este apéndice contiene un breve resumen de los métodos para resolver ecuaciones lineales y no lineales,. y es sólo eso: un resumen. Los detalles pueden consultarse en cualquiera de los numerosos textos sobre el análisis numérico que se encuentran en cualquier biblioteca.

Si escribimos varios balances de materia lineales, digamos m de ellos, tendrán la forma

Figura Calores de vaporización de hidrocarburos y fracciones del petróleo a presión atmosférica de 1.0 atm

Figura Propiedades de las fracciones del petróleo

Figura Calor de combustión de aceites combustibles y fracciones del petróleo

Figura Presión de vapor de hidrocarburos

Tabla Calores Específicos de hidrocarburos líquidos

Propiedades físicas de fracciones de petroleo (IV)

En la tabla K.2 se muestra la fuente, la base para el punto de ebullición y las limitaciones especiales de los diversos diagramas de este apéndice. Si se van a utilizar en cálculos asistidos por computadora, consulte el apéndice del Suplemento que viene en el disco que acompaña este libro.

Propiedades físicas de fracciones de petroleo (III)

En este apéndice se usan otros promedios de puntos de ebullición para evaluar K y otras propiedades físicas. (Consulte Daubert o Miquel si desea los detalles) Este factor se ha relacionado con muchos de los otros ensayos sencillos y propiedades de las fracciones del petróleo, como la viscosidad, el peso molecular, la temperatura crítica y el porcentaje de hidrógeno, de modo que es muy fácil estimar el factor para una muestra en particular. Además hay tablas del factor de caracterización UOP para una amplia variedad de fracciones del petróleo comunes, como se muestra en la tabla K.1 para líquidos representativos.

Propiedades físicas de fracciones de petroleo (II)

Con el paso de los años, se han extendido diversas fases de los trabajos iniciales y está apareciendo un nuevo esquema de caracterización basado en el enfoque de pseudocompuestos. Daubert resume los métodos tradicionales y nuevos respecto a la predicción de pesos moleculares, temperatura y presión pseudo críticas, factor acéntrico y factores de caracterización.

En este apéndice presentamos los resultados de los trabajos de Smith y Watson y colaboradores, quienes relacionaron las propiedades de petróleo con un factor llamado factor de caracterización (o a veces factor de caracterización UOP) que se define como:

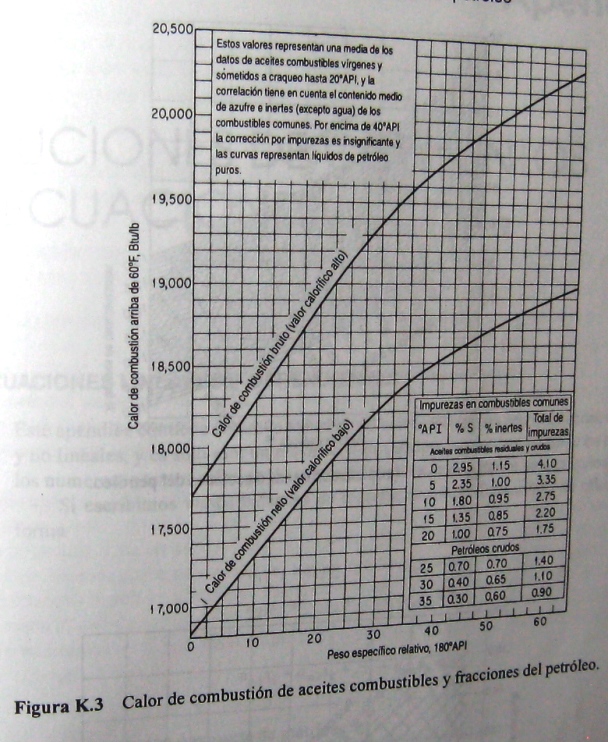
Propiedades físicas de fracciones de petroleo (I)

A principios de la década de 1930 se establecieron ensayos para caracterizar los tipos de petróleo y las fracciones del petróleo, con objeto de relacionar diversas características de los productos del petróleo con dichos ensayos. Los detalles de los ensayos se pueden consultar en Petroleum Products and Lubricants, la publicación anual del Comité D-2 de la American Society for Testing Materials. Estos ensayos no son científicamente exactos, así que es indispensable seguir al pie de la letra los procedimientos establecidos en las pruebas si se desea obtener resultados confiables. No obstante lo anterior, se han adoptado estos ensayos porque son muy fáciles de realizar en un laboratorio ordinaria y porque permiten predecir las propiedades de las fracciones de petróleo a partir de los resultados. Las especificaciones para combustibles, aceites, etc., se presentan en términos de estos ensayos junto con muchas otras propiedades, como el punto de inflamación, el porcentaje de azufre y la viscosidad.

Diagrama de presión-entalpía para el dióxido de carbono

Diagrama de presión-entalpia para el tolueno

Diagrama de entalpía-concentración del sistema ácido sulfúrico-agua relativo a los componentes puros