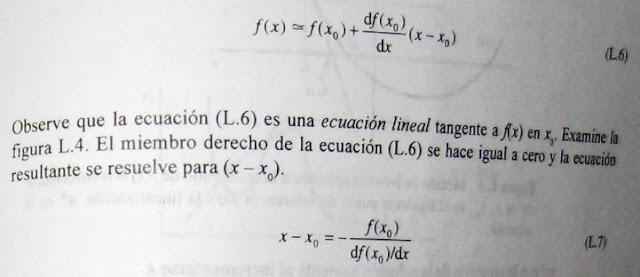Los métodos de Wegstein y de Eigenvalor Dominante enumerados en la figura L.3 son técnicas útiles para acelerar la convergencia (o evitar la no convergencia) del método de sustituciones sucesivas. Consulte las referencias citadas en dicha figura si desea detalles específicos.
El método de Wegstein, que se usa en muchos programas de simulación de procesos, acelera la convergencia del método de sustituciones sucesivas en cada iteración. En el método de la secante, la pendiente aproximada es
Etiquetas
Buscador
miércoles, 17 de agosto de 2016
Métodos de Brent y de Brown (I)
Los métodos de Brent y de Brown son variaciones del método de Newton que mejoran la convergencia. SE mezclan el cálculo de los elementos de Jk de la ecuación (L.11) ya resolución de las ecuaciones lineales. Se obtiene cada fila de Jk según se va necesitando.
Para que el procedimiento de sustitución sucesiva converja siempre, es necesario que el valor del eigenvalor absoluto más grande de la matriz jacobiana de F(x) evaluado en cada punto de iteración sea menor que (o igual a) uno. Si existe más de una solución para las ecuaciones (L.7), el vector inicial y la selección de la variable para la cual se resolverá cada ecuación controlan la solución obtenida. Además, podemos obtener diferentes resultados de convergencia dependiendo de la disposición de las ecuaciones y de la elección de la variable para la cual resolver.
miércoles, 3 de agosto de 2016
Métodos de la secante (III)
La aplicación de la ecuación (L.14) produce los siguientes resultados para f(x) = 4x³ - 1 = 0 comenzando con xk = -3 y xq = 3. En seguida mostramos algunos de los valores de f(x) y x durante la búsqueda; observa que xq no cambia a fin de mantener la delimitación con f(x) > 0
martes, 2 de agosto de 2016
Métodos de la secante (II)
Los métodos de la secante se utilizan inicialmente dos puntos xk y xq que abarcan el intervalo de x y corresponden a puntos en los que los valores de f(x) tienen signos opuestos. El cero de f(x) queda predicho por
Los dos puntos retenidos para el siguiente paso son x y xq o bien xk; la elección se hace de modo que el par de valores f(x) y f(xk) o bien f(xq) tengan signos opuestos a fin de mantener la delimitación de x*. (Esta variación se denomina "regula falsi" o método de la posición falsa). En la figura 1.6, para (k+1)ésima etapa se escogerían x y xq como extremos de la línea secante. Es posible que los métodos de secante parezcan burdos, pero funcionan bien en la práctica. Los detalles de los aspectos computacionales de un buen algoritmo de resolución de múltiples ecuaciones por el método de la secante son demasiado extensos para bosquejarlos aquí (sobre todo el cálculo de una nueva matriz jacobiana a partir de la anterior; consulte Dennis y Schnabel).
Los dos puntos retenidos para el siguiente paso son x y xq o bien xk; la elección se hace de modo que el par de valores f(x) y f(xk) o bien f(xq) tengan signos opuestos a fin de mantener la delimitación de x*. (Esta variación se denomina "regula falsi" o método de la posición falsa). En la figura 1.6, para (k+1)ésima etapa se escogerían x y xq como extremos de la línea secante. Es posible que los métodos de secante parezcan burdos, pero funcionan bien en la práctica. Los detalles de los aspectos computacionales de un buen algoritmo de resolución de múltiples ecuaciones por el método de la secante son demasiado extensos para bosquejarlos aquí (sobre todo el cálculo de una nueva matriz jacobiana a partir de la anterior; consulte Dennis y Schnabel).
lunes, 1 de agosto de 2016
Métodos de la secante (I)
En el método de la secante el modelo aproximado análogo al miembro derecho de la ecuación (L.6) (igualado a cero) es
Así, el método de la secante imita al método de Newton (en este sentido el método de la secante también es un método cuasi-Newton)
Así, el método de la secante imita al método de Newton (en este sentido el método de la secante también es un método cuasi-Newton)
domingo, 31 de julio de 2016
Método cuasi-Newton (I)
En la ecuación L.12 se usó una diferencia central pero pueden servir diferencias hacia adelante o cualquier otro esquema de diferencias siempre que el tamaño de paso h se escoja de modo que sea apropiado para la fórmula de diferencias y la precisión de la computadora en la cual se ejecutarán los cálculos.
Aparte de los problemas de seleccionar el valor de h, la única desventaja de los métodos cuasi-Newton es que se requieren evaluaciones adicionales de la función en cada iteración k. La ecuación (L.12) se puede aplicar a conjuntos de ecuaciones si las derivadas parciales se reemplazaran por aproximaciones de diferencias finitas.
sábado, 9 de julio de 2016
Método cuasi-Newton (I)
En general, un método cuasi-Newton es aquel que imita el método de Newton, Si f(x) no está dada por una fórmula, o si la fórmula es tan complicada que no es posible formular derivadas análiticas, se puede sustituir df/dx en la ecuación (L.7) por una aproximación de diferencias finitas
viernes, 8 de julio de 2016
Ecuaciones no lineales independientes - Método de Newton (VI)
El análogo de (L.10) en notación de matrices es
donde J es la matriz jacobiana (la matriz cuyos elementos consisten en las primeras derivadas parciales de las ecuaciones respecto de las variables). Para dos ecuaciones
Jk(x-xk) = -f(xk)
jueves, 7 de julio de 2016
Ecuaciones no lineales independientes - Método de Newton (V)
EStas ecuaciones son lineales y se pueden resolver mediante un programa de resolución de ecuaciones lineales para obtener el siguiente punto de refencia (x11, x21). Se continúa la iteración hasta lograr una solución con una precisión satisfactoria. Desde luego, cabe la posibilidad de no llegar a ninguna solución, como se ilustra en la figura L.5c, o de no obtener la a causa de errores de redondeo o truncado. Si la matriz jacobiana (véase la ecuación (L.11) más adelante) es singular, las ecuaciones linealizadas tal vez no tengan solución o tengan una familia de soluciones, y lo más probable es que no se pueda obtener una solución con el método de Newton. ES muy común que la matriz jacobiana está male determinada porque si x0 está lejos de la solución o las ecuaciones no lineales tienen una escala deficiente no se obtendrá la solución correcta.
miércoles, 6 de julio de 2016
Ecuaciones no lineales independientes - Método de Newton (IV)
Suponga que tiene las siguientes dos ecuaciones independientes de dos variables cuyos valores necesita determinar:
martes, 5 de julio de 2016
lunes, 4 de julio de 2016
Ecuaciones no lineales independientes - Método de Newton (II)
Por ejemplo, suponga que f(x) = 4x^3 - 1 = 0, de modo que df(x)/dx = 12x^2. La secuencia de pasos para aplicar el método de Newton usando la ecuación (L.7) y comenzando en xo = 3 sería
domingo, 3 de julio de 2016
Ecuaciones no lineales independientes - Método de Newton (I)
Refiérase a las ecuaciones (L.5). Para una sola ecuación (y variable), f(x) = 0, el método de Newton utiliza la expansión de f(x) en una serie de Taylor alrededor de un punto de referencia (una estimación inicial para la solución) xo.
sábado, 2 de julio de 2016
Ecuaciones no lineales independientes (II)
En la figura L.3 se clasifican los principales métodos generales de resolución de sistemas de ecuaciones no lineales. Dentro de cada categoría y combinando categorías podemos encontrar innumerables variaciones y submétodos en la literatura disponibles como códigos para computadora.
miércoles, 29 de junio de 2016
Ecuaciones no lineales independientes (I)
Los criterios precisos que se usan para comprobar si un sistema lineal de ecuaciones ésta determinado no se pueden extender sin más a los sistemas de ecuaciones no lineales. Además, la resolución de conjuntos de ecuaciones no lineales requiere el empleo de códigos de computadora que tal vez no puedan resolver el problema por diversas razones, algunas de las cuales mencionaremos aquí. El problema por resolver se puede escribir como:
donde cada función f1(x1,......, xn) corresponde a una función no lineal que contiene una o más de las variables cuyo valor se desconoce.
donde cada función f1(x1,......, xn) corresponde a una función no lineal que contiene una o más de las variables cuyo valor se desconoce.
martes, 28 de junio de 2016
Ecuaciones no homogéneas - ejemplo 3
El número de componentes independientes no siempre es igual al número de especies atómicas, como se muestra en el siguiente ejemplo.
Determine el número de componentes independientes para un proceso en el que interviene la siguiente reacción:
Determine el número de componentes independientes para un proceso en el que interviene la siguiente reacción:
jueves, 23 de junio de 2016
Ecuaciones no homogéneas - ejemplo 2
Determine el número de componentes independientes (que es igual al número de balances de materia independientes) para un proceso en el que intervienen las dos reacciones en competencia siguientes:
miércoles, 22 de junio de 2016
Ecuaciones no homogéneas - ejemplo 1
Con objeto de ilustrar las operaciones elementales requeridas para aplicar el método de Gauss-Jordan, consideremos el siguiente conjunto de tres ecuaciones independientes con tres incógnitas:
martes, 21 de junio de 2016
Ecuaciones no homogéneas r > n (II)
En general, hay dos formas de resolver la ecuación (L.3) para x1,.......,x3: técnicas de eliminación y técnicas iterativas. Ambas se ejecutan fácilmente con la ayuda de programas para computadora. En la contraportada del libro el lector encontrará un disco con programas que pueden usarse para resolver conjuntos de ecuaciones lineales. Ilustraremos el método de eliminación de Gauss-Jordan. El lector puede encontrar otras técnicas en textos sobre matrices, álgebra lineal y análisis numérico.
La esencia del método de Gauss-Jordan consiste en transformar la ecuación (L.3) en la ecuacion (L.4) mediante operaciones elemantales secuenciales no únicas sobre la ecuación (L.3).
La esencia del método de Gauss-Jordan consiste en transformar la ecuación (L.3) en la ecuacion (L.4) mediante operaciones elemantales secuenciales no únicas sobre la ecuación (L.3).
lunes, 20 de junio de 2016
domingo, 19 de junio de 2016
sábado, 18 de junio de 2016
viernes, 17 de junio de 2016
jueves, 16 de junio de 2016
Ecuaciones lineales independientes (IV)
Si ésta no es cuadrada, se buscará el determinante distinto de cero para la mayor de las matrices cuadradas que pueden formarse a partir de A. Es necesario verificar todas las posibles submatrices de A. Utilizaremos números enteros como elementos en las matrices que siguen. Los números no enteros pueden conducir a resultados menos claros en lo que toca a la verificación de si el valor de un determinante es cero o no.
Se r = número de ecuaciones independientes
n = número de variables cuyo valor se desconoce.
Se r = número de ecuaciones independientes
n = número de variables cuyo valor se desconoce.
miércoles, 15 de junio de 2016
Ecuaciones lineales independientes (III)
La figura L.2 representa cada uno de estos casos de forma geométrica en dos dimensiones. El caso 1 por lo regular se considera inconsistente, en tanto que los casos 2 y 3 son consistentes. Sin embargo, para un ingeniero interesado en la resolución de problemas prácticos, el caso 3 es tan insatisfactorio como el caso 1. Por tanto, llamaremos el caso 2 determinado, y el caso 3 se calificará como indeterminado.
Para asegurar que un sistema de ecuaciones representando por (L.1) tenga una solución única, es necesario demostrar primero que que (L.1) es consistente, esto es, que la matriz de coeficiones A y la matriz aumentada [A, b] tienen el mismo rango, r. Entonces, si n = r, el sistema (L.1) será determinado. Por otro lado, si r < n, como puede suceder, será necesario especificar de alguna manera (n - r) variables, o fijarlas mediante procedimientos de optimización. Si las ecuaciones son independientes, m = r. Si calculamos el orden del determinante distinto de cero más grande de una matriz dada, podemos determinar el rango de es matriz.
Para asegurar que un sistema de ecuaciones representando por (L.1) tenga una solución única, es necesario demostrar primero que que (L.1) es consistente, esto es, que la matriz de coeficiones A y la matriz aumentada [A, b] tienen el mismo rango, r. Entonces, si n = r, el sistema (L.1) será determinado. Por otro lado, si r < n, como puede suceder, será necesario especificar de alguna manera (n - r) variables, o fijarlas mediante procedimientos de optimización. Si las ecuaciones son independientes, m = r. Si calculamos el orden del determinante distinto de cero más grande de una matriz dada, podemos determinar el rango de es matriz.
martes, 14 de junio de 2016
Ecuaciones lineales independientes (II)
Con m ecuaciones de n variables incógnitas podemos distinguir tres casos:
- No existe un conjunto de x que satisfaga la ecuación (L.1)
- Existe un conjunto único de x que satisface la ecuación (L.1)
- Existe un número infinito de conjuntos de x que se satisfacen la ecuación (L.1)
lunes, 13 de junio de 2016
Ecuaciones lineales independientes (I)
Este apéndice contiene un breve resumen de los métodos para resolver ecuaciones lineales y no lineales,. y es sólo eso: un resumen. Los detalles pueden consultarse en cualquiera de los numerosos textos sobre el análisis numérico que se encuentran en cualquier biblioteca.
Si escribimos varios balances de materia lineales, digamos m de ellos, tendrán la forma
Si escribimos varios balances de materia lineales, digamos m de ellos, tendrán la forma
domingo, 12 de junio de 2016
sábado, 11 de junio de 2016
viernes, 10 de junio de 2016
jueves, 9 de junio de 2016
miércoles, 8 de junio de 2016
martes, 7 de junio de 2016
Propiedades físicas de fracciones de petroleo (IV)
En la tabla K.2 se muestra la fuente, la base para el punto de ebullición y las limitaciones especiales de los diversos diagramas de este apéndice. Si se van a utilizar en cálculos asistidos por computadora, consulte el apéndice del Suplemento que viene en el disco que acompaña este libro.
lunes, 6 de junio de 2016
Propiedades físicas de fracciones de petroleo (III)
En este apéndice se usan otros promedios de puntos de ebullición para evaluar K y otras propiedades físicas. (Consulte Daubert o Miquel si desea los detalles) Este factor se ha relacionado con muchos de los otros ensayos sencillos y propiedades de las fracciones del petróleo, como la viscosidad, el peso molecular, la temperatura crítica y el porcentaje de hidrógeno, de modo que es muy fácil estimar el factor para una muestra en particular. Además hay tablas del factor de caracterización UOP para una amplia variedad de fracciones del petróleo comunes, como se muestra en la tabla K.1 para líquidos representativos.
domingo, 5 de junio de 2016
Propiedades físicas de fracciones de petroleo (II)
Con el paso de los años, se han extendido diversas fases de los trabajos iniciales y está apareciendo un nuevo esquema de caracterización basado en el enfoque de pseudocompuestos. Daubert resume los métodos tradicionales y nuevos respecto a la predicción de pesos moleculares, temperatura y presión pseudo críticas, factor acéntrico y factores de caracterización.
En este apéndice presentamos los resultados de los trabajos de Smith y Watson y colaboradores, quienes relacionaron las propiedades de petróleo con un factor llamado factor de caracterización (o a veces factor de caracterización UOP) que se define como:
En este apéndice presentamos los resultados de los trabajos de Smith y Watson y colaboradores, quienes relacionaron las propiedades de petróleo con un factor llamado factor de caracterización (o a veces factor de caracterización UOP) que se define como:
sábado, 4 de junio de 2016
Propiedades físicas de fracciones de petroleo (I)
A principios de la década de 1930 se establecieron ensayos para caracterizar los tipos de petróleo y las fracciones del petróleo, con objeto de relacionar diversas características de los productos del petróleo con dichos ensayos. Los detalles de los ensayos se pueden consultar en Petroleum Products and Lubricants, la publicación anual del Comité D-2 de la American Society for Testing Materials. Estos ensayos no son científicamente exactos, así que es indispensable seguir al pie de la letra los procedimientos establecidos en las pruebas si se desea obtener resultados confiables. No obstante lo anterior, se han adoptado estos ensayos porque son muy fáciles de realizar en un laboratorio ordinaria y porque permiten predecir las propiedades de las fracciones de petróleo a partir de los resultados. Las especificaciones para combustibles, aceites, etc., se presentan en términos de estos ensayos junto con muchas otras propiedades, como el punto de inflamación, el porcentaje de azufre y la viscosidad.
viernes, 3 de junio de 2016
jueves, 2 de junio de 2016
miércoles, 1 de junio de 2016
Diagrama de entalpía-concentración del sistema ácido sulfúrico-agua relativo a los componentes puros
martes, 31 de mayo de 2016
sábado, 28 de mayo de 2016
viernes, 27 de mayo de 2016
jueves, 4 de febrero de 2016
miércoles, 3 de febrero de 2016
miércoles, 20 de enero de 2016
martes, 19 de enero de 2016
domingo, 17 de enero de 2016
sábado, 16 de enero de 2016
viernes, 15 de enero de 2016
jueves, 14 de enero de 2016
Suscribirse a:
Entradas (Atom)